Производная икса равна. Производная

Производная - главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x

Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Наиболее употребительны следующие обозначения производной :

Пример 1. Пользуясь определением производной , найти производную функции

Решение. Из определения производной вытекает следующая схема её вычисления.

Дадим аргументу приращение (дельта) и найдём приращение функции:

Найдём отношение приращения функции к приращению аргумента:

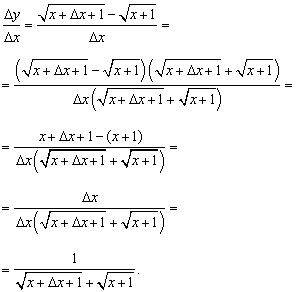
Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:

Физический смысл производной

К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле - задачи о мгновенной скорости неравномерного прямолинейного движения точки.

Пусть камешек поднят и затем из состояния покоя отпущен. Путь s , проходимый за время t , является функцией времени, то есть. s = s (t ). Если задан закон движения точки, то можно определить среднюю скорость за любой промежуток времени. Пусть в момент времени камешек находился в положении A , а в момент - в положении B . За промежуток времени (от t до ) точка прошла путь . Поэтому средняя скорость движения за этот промежуток времени, которую обзначим через , составляет

.

Однако движение свободно падающего тела явно неравномерное. Скорость v падения постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути. Такая характеристика тем точнее, чем меньше промежуток времени . Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени t ) называется предел средней скорости при :

(при условии, что этот предел существует и конечен).

Так выясняется, что мгновенная скорость есть предел отношения приращения функции s (t ) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.

.

Решение обозначенной задачи представляет собой физический смысл производной . Итак, производной функции y=f (x ) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Пример 2. Найти производную функции

Решение. Из определения производной вытекает следующая схема для её вычисления.

Шаг 1. Дадим аргументу приращение и найдём

Шаг 2. Найдём приращение функции:

Шаг 3. Найдём отношение приращения функции к приращению аргумента:

Шаг 4. Вычислим предел этого отношения при , то есть производную:

Геометрический смысл производной

Пусть функция определена на интервале и пусть точка М на графике функции соответствует значению аргумента , а точка Р – значению . Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .

Если существует

проходящую через точку , называют предельным положением секущей МР при (или при ).

Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .

Из определения следует, что для существования касательной достаточно, чтобы существовал предел

,

причём предел равен углу наклона касательной к оси .

Теперь дадим точное определение касательной.

Касательной к графику функции в точке называется прямая, проходящая через точку и имеющая угловой коэффициент , т.е. прямая, уравнение которой

Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x . В этом состоит геометрический смысл производной.

Составить отношение и вычислить предел .

Откуда появилась таблица производных и правила дифференцирования ? Благодаря единственному пределу . Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных , оттачивая алгоритм и технические приёмы решения:

Пример 1

По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: .

Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.

Рассмотрим некоторую (конкретную) точку , принадлежащую области определения функции , в которой существует производная. Зададим в данной точке приращение (разумеется, не выходящее за рамки о/о -я) и составим соответствующее приращение функции:

Вычислим предел:

Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим числитель и знаменатель на сопряженное выражение :

Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций .

Поскольку в качестве можно выбрать ЛЮБУЮ точку интервала , то, осуществив замену , получаем:

Ответ

В который раз порадуемся логарифмам:

Пример 2

Найти производную функции , пользуясь определением производной

Решение : рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от подстрочного индекса и вместо буквы использовать букву .

Рассмотрим произвольную точку , принадлежащую области определения функции (интервалу ), и зададим в ней приращение . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.

Тогда соответствующее приращение функции:

Найдём производную:

Простота оформления уравновешивается путаницей, которая может возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: – античная статуя, а – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».

Устранение неопределённости закомментирую пошагово:

(1) Используем свойство логарифма .

(2) В скобках почленно делим числитель на знаменатель.

(3) В знаменателе искусственно домножаем и делим на «икс» чтобы воспользоваться замечательным пределом , при этом в качестве бесконечно малой величины выступает .

Ответ : по определению производной:

Или сокращённо:

Предлагаю самостоятельно сконструировать ещё две табличные формулы:

Пример 3

В данном случае составленное приращение сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).

Пример 3: Решение : рассмотрим некоторую точку , принадлежащую области определения функции . Зададим в данной точке приращение и составим соответствующее приращение функции:

Найдём производную в точке :

Так как в качестве можно выбрать любую точку области определения функции , то и
Ответ : по определению производной

Пример 4

Найти производную по определению

А тут всё необходимо свести к замечательному пределу . Решение оформлено вторым способом.

Аналогично выводится ряд других табличных производных . Полный список можно найти в школьном учебнике, или, например, 1-м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены формулой .

Пример 4: Решение , принадлежащую , и зададим в ней приращение

Найдём производную:

Используем замечательный предел

Ответ : по определению

Пример 5

Найти производную функции , используя определение производной

Решение : используем первый стиль оформления. Рассмотрим некоторую точку , принадлежащую , изададим в ней приращение аргумента . Тогда соответствующее приращение функции:

Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение . Берём точку (число) и находим в ней значение функции: , то есть в функцию вместо «икса» следует подставить . Теперь берём тоже вполне конкретное число и так же подставляем его в функцию вместо «икса»: . Записываем разность , при этом необходимо полностью взять в скобки .

Составленное приращение функции бывает выгодно сразу же упростить . Зачем? Облегчить и укоротить решение дальнейшего предела.

Используем формулы , раскрываем скобки и сокращаем всё, что можно сократить:

Индейка выпотрошена, с жаркое никаких проблем:

Поскольку в качестве можно выбрать любое действительное число, то проведём замену и получим .

Ответ : по определению.

В целях проверки найдём производную с помощью правил дифференцирования и таблицы :

Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.

Пример 6

Найти производную функции по определению производной

Это пример для самостоятельного решения. Результат лежит на поверхности:

Пример 6: Решение : рассмотрим некоторую точку , принадлежащую , и зададим в ней приращение аргумента . Тогда соответствующее приращение функции:


Вычислим производную:


Таким образом:
Поскольку в качестве можно выбрать любое действительное число, то и
Ответ : по определению.

Вернёмся к стилю №2:

Пример 7

Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции :

Решение : рассмотрим произвольную точку , принадлежащую , зададим в ней приращение аргумента и составим приращение функции:

Найдём производную:


(1) Используем тригонометрическую формулу .

(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.

(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.

(4) В силу нечётности синуса выносим «минус». Под косинусом указываем, что слагаемое .

(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел . Таким образом, неопределённость устранена, причёсываем результат.

Ответ : по определению

Как видите, основная трудность рассматриваемой задачи упирается в сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».

Пример 8

Пользуясь определением, найти производную функции

Пример 8: Решение : рассмотрим произвольную точку , принадлежащую , зададим в ней приращение и составим приращение функции:

Найдём производную:

Используем тригонометрическую формулу и первый замечательный предел:


Ответ : по определению

Разберём более редкую версию задачи:

Пример 9

Найти производную функции в точке , пользуясь определением производной.

Во-первых, что должно получиться в сухом остатке? Число

Вычислим ответ стандартным способом:

Решение : с точки зрения наглядности это задание значительно проще, так как в формуле вместо рассматривается конкретное значение.

Зададим в точке приращение и составим соответствующее приращение функции:

Вычислим производную в точке:

Используем весьма редкую формулу разности тангенсов и в который раз сведём решение к первому замечательному пределу :

Ответ : по определению производной в точке.

Задачу не так трудно решить и «в общем виде» – достаточно заменить на или просто в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.

Пример 10

Используя определение, найти производную функции в точке (одно из которых может оказаться и бесконечным) , о котором я в общих чертах уже рассказал на теоретическом уроке о производной .

Некоторые кусочно-заданные функции дифференцируемы и в точках «стыка» графика, например, котопёс обладает общей производной и общей касательной (ось абсцисс) в точке . Кривой, да дифференцируемый на ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.

©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-06-11

Урок на тему: "Что такое производная? Определение производной"

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда "1С: Математический конструктор 6.1"

Что будем изучать:
1. Введение в понятие производной.
2. Чуть-чуть истории.

4. Производная на графике функции. Геометрический смысл производной.

6. Дифференцирование функции.
7. Примеры.

Введение в понятие производной

Существует множество задач совершенно разных по смыслу, но при этом есть математические модели, которые позволяют рассчитывать решения наших задач совершенно одинаковым способом. Например, если рассмотреть такие задачи как:

А) Есть некоторый счет в банке, который постоянно изменяется один раз в несколько дней, сумма постоянно растет, требуется найти с какой скоростью растет счет.
б) Завод выпускает конфеты, есть некоторый постоянный прирост выпуска конфет, найти насколько быстро увеличивается прирост конфет.
в) Скорость движения автомобиля в некоторый момент времени t, если известно положение автомобиля, и он движется по прямой линии.
г) Нам дан график функции и в некоторой точке к нему проведена касательная, требуется найти тангенс угла наклона к касательной.
Формулировка наших задач совершенно разная, и, кажется, что они решаются совершенно разными способами, но математики придумали как можно решить все эти задачи совершенно одинаковым способом. Было введено понятие производной.

Чуть-чуть истории

Термин производная ввел великий математик – Лагранж, перевод на русский язык получается из французского слова derivee, он же и ввел современные обозначения производной которые мы рассмотрим позже.
Рассматривали понятие производной в своих работах Лейбниц и Ньютон, применение нашему термину они находили в геометрии и механики соответственно.
Чуть позже мы с вами узнаем, что производная определяется через предел, но существует небольшой парадокс в истории математики. Математики научились считать производную раньше, чем ввели понятие предела и собственно поняли, что же такое производная.

Пусть функция y=f(x) определена на некотором интервале, содержащим внутри себя некоторую точку x0. Приращение аргумента Δx – не выходит из нашего интервала. Найдем приращение Δy и составим отношение Δy/Δx, если существует предел этого отношения при Δx стремящимся к нулю, то указанный предел называют производной функции y=f(x) в точке x0 и обозначают f’(x0).

Попробуем объяснить, что такое производная не математическим языком:
На математическом языке: производная - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
На обычном языке: производная – скорость изменения функции в точке x0.
Давайте посмотрим на графики трех функций:

Ребята, как вы думаете, какая из кривых растет быстрее?
Ответ, кажется, очевиден всем 1 кривая растет быстрее остальных. Мы смотрим, насколько круто идет вверх график функции. Другими словами - насколько быстро меняется ордината при изменении х. Одна и та же функция в разных точках может иметь разное значение производной - то есть может меняться быстрее или медленнее.

Производная на графике функции. Геометрический смысл производной

Теперь давайте посмотрим, как же найти производную с помощью графиков функции:


Посмотрим на наш график функции: Проведём в точке c абсциссой x0 касательную к графику функции. Касательная и график нашей функции соприкасаются в точке А. Нам надо оценить, насколько круто вверх идет график функции. Удобная величина для этого - тангенс угла наклона касательной.

Определение. Производная функции в точке x0 равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Угол наклона касательной выбирается как угол между касательной и положительным направлением оси абсцисс.
И так производная нашей функции равна:

И так производная в точке x0 равна тангенсу угла наклона касательной, это геометрический смысл производной.

Алгоритм нахождения производной функции y=f(x).
а) Зафиксировать значение x, найти f(x).
б) Найти приращение аргумента x+ Δx, и значение приращения функции f(x+ Δx).
в) Найти приращение функции Δy= f(x+ Δx)-f(x).
г) Составить соотношение: Δy/Δx
д) Вычислить

Это и есть производная нашей функции.

Дифференцирование функции

Если функции y=f(x)имеет производную в точке x, то ее называют дифференцируемой в точке x. Процесс нахождения производной называют дифференцированием функции y=f(x).
Вернемся к вопросу непрерывности функции. Если функция дифференцируема в некоторой точке, тогда к графику функции в этой точке можно провести касательную, функция не может иметь разрыв в этой точки, тогда просто напросто нельзя провести касательную.
И так запишем выше сказанное как определение:
Определение. Если функция дифференцируема в точке x, то она непрерывна в этой точке.
Однако, если функция непрерывна в точке, то это не значит, что она дифференцируема в этой точке. Например, функция y=|x| в точке x=0 непрерывна, но касательную провести нельзя, а значит и производной не существует.

Примеры производной

Найти производную функции: y=3x
Решение:
Будем пользоваться алгоритмом поиска производной.
1) Для фиксированного значения x, значение функции y=3x
2) В точке x+ Δx, y=f(x+ Δx)=3(x+ Δx)=3x+3 Δx

3) Найдем приращение функции: Δy= f(x+ Δx)-f(x)= 3x+3 Δx-3x=3Δ

Доказательство и вывод формул производной экспоненты (e в степени x) и показательной функции (a в степени x). Примеры вычисления производных от e^2x, e^3x и e^nx. Формулы производных высших порядков.

Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′ = e x .

Производная показательной функции с основанием степени a равна самой функции, умноженной на натуральный логарифм от a :
(2) .

Вывод формулы производной экспоненты, e в степени x

Экспонента - это показательная функция, у которой основание степени равно числу e , которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.

Вывод формулы производной экспоненты

Рассмотрим экспоненту, e в степени x :
y = e x .
Эта функция определена для всех . Найдем ее производную по переменной x . По определению, производная является следующим пределом:
(3) .

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
А) Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь - некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .

Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.

Сделаем подстановку . Тогда ; .
В силу непрерывности экспоненты,
.
Поэтому при , . В результате получаем:
.

Сделаем подстановку . Тогда . При , . И мы имеем:
.

Применим свойство логарифма (5):
. Тогда
.

Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.

Тем самым мы получили формулу (1) производной экспоненты.

Вывод формулы производной показательной функции

Теперь выведем формулу (2) производной показательной функции с основанием степени a . Мы считаем, что и . Тогда показательная функция
(8)
Определена для всех .

Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции и логарифма .
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.

Производные высших порядков от e в степени x

Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
(1) .

Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.

Отсюда видно, что производная n-го порядка также равна исходной функции:
.

Производные высших порядков показательной функции

Теперь рассмотрим показательную функцию с основанием степени a :
.
Мы нашли ее производную первого порядка:
(15) .

Дифференцируя (15), получаем производные второго и третьего порядка:
;
.

Мы видим, что каждое дифференцирование приводит к умножению исходной функции на . Поэтому производная n-го порядка имеет следующий вид:
.

Содержание статьи

ПРОИЗВОДНАЯ –производной функции y = f (x ), заданной на некотором интервале (a , b ) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Производную принято обозначать так:

Широко употребляются и другие обозначения:

Мгновенная скорость.

Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M 0 , зависит от времени t , т.е. s есть функция времени t : s = f (t ). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M 0, а в некоторый следующий момент t + Dt оказалась в положении M 1 – на расстоянии s + Ds от начального положения (см. рис .).

Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds . В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds .

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t . Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t . Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt . Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt , когда приращение времени стремится к нулю. Так как

Геометрическое значение производной. Касательная к графику функции.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления .

Пусть кривая есть график функции y = f (x ) в прямоугольной системе координат (см . рис.).

При некотором значении x функция имеет значение y = f (x ). Этим значениям x и y на кривой соответствует точка M 0(x , y ). Если аргументу x дать приращение Dx , то новому значению аргумента x + Dx соответствует новое значение функции y+ Dy = f (x + Dx ). Соответствующей ему точкой кривой будет точка M 1(x + Dx , y + Dy ). Если провести секущую M 0M 1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox , из рисунка непосредственно видно, что .

Если теперь Dx стремится к нулю, то точка M 1 перемещается вдоль кривой, приближаясь к точке M 0, и угол j изменяется с изменением Dx . При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M 0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:

Следовательно, f ´(x ) = tga

т.е. значение производной f ´(x ) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f (x ) в соответствующей точке M 0(x ,y ) с положительным направлением оси Ox .

Дифференцируемость функций.

Определение. Если функция y = f (x ) имеет производную в точке x = x 0, то функция дифференцируема в этой точке.

Непрерывность функции, имеющей производную. Теорема.

Если функция y = f (x ) дифференцируема в некоторой точке x = x 0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x 0 функция y = f (x ) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x | непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f (x ) непрерывна на отрезке [a ,b ], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f (a ) = f (b ) = 0), то внутри отрезка [a ,b ] существует, по крайней мере одна, точка x = с , a c b, в которой производная f ў(x ) обращается в нуль, т.е. f ў(c ) = 0.

Теорема о конечных приращениях (теорема Лагранжа). Если функция f (x ) непрерывна на отрезке [a , b ] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a , b ] найдется по крайней мере одна точка с , a c b, что

f (b ) – f (a ) = f ў(c )(b – a ).

Теорема об отношении приращений двух функций (теорема Коши). Если f (x ) и g (x ) – две функции, непрерывные на отрезке [a , b ] и дифференцируемые во всех внутренних точках этого отрезка, причем g ў(x ) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a , b ] найдется такая точка x = с , a c b, что

Производные различных порядков.

Пусть функция y = f (x ) дифференцируема на некотором отрезке [a , b ]. Значения производной f ў(x ), вообще говоря, зависят от x , т.е. производная f ў(x ) представляет собой тоже функцию от x . При дифференцировании этой функции получается так называемая вторая производная от функции f (x ), которая обозначается f ўў (x ).

Производной n- го порядка от функции f (x ) называется производная (первого порядка) от производной n- 1- го и обозначается символом y (n ) = (y (n – 1))ў.

Дифференциалы различных порядков.

Дифференциал функции y = f (x ), где x – независимая переменная, есть dy = f ў(x )dx , некоторая функция от x , но от x может зависеть только первый сомножитель f ў(x ), второй же сомножитель (dx ) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x , то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d 2y :

d (dx ) = d 2y = f ўў(x )(dx ) 2 .

Дифференциалом n- го порядка называется первый дифференциал от дифференциала n- 1- го порядка:

d n y = d (d n –1 y ) = f (n )(x )dx (n ).

Частная производная.

Если функция зависит не от одного, а от нескольких аргументов x i (i изменяется от 1 до n , i = 1, 2,… n ), f (x 1, x 2,… x n ), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, x i . Частная производная 1-ого порядка по x i определяется как обычная производная, при этом предполагается, что все аргументы, кроме x i , сохраняют постоянные значения. Для частных производных вводятся обозначения

Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.

Анна Чугайнова